The brand new prove it After School Club

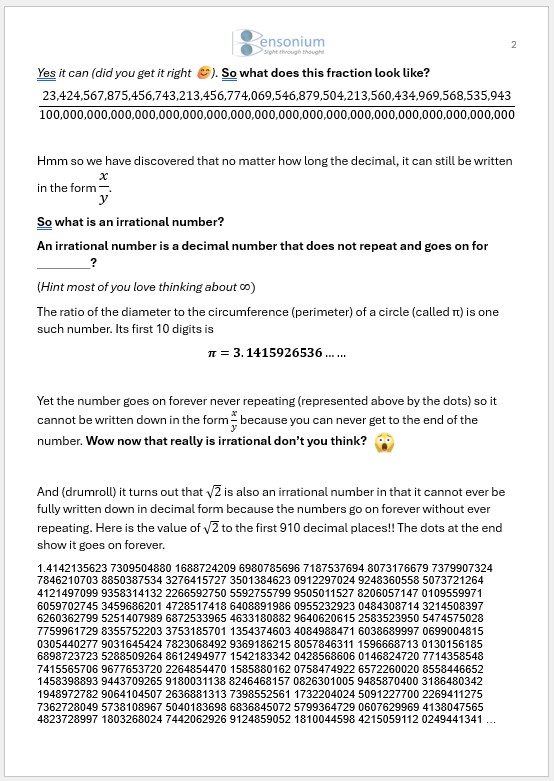I begin by imagining that our proof is like baking a mathematical cake where we combine key ingredients to achieve our objective. The important ingredients we need are algebra, maths functions, the concept of a proof by contradiction, and an understanding that fractions with even numbers in their numerator and denominator are like zombies in that they don’t really exist because they can be unmasked by factoring out 2. We then start reminding them of the rules of basic algebra before introducing them to the concept of a mathematical function via a dressing up game. Through the dressing up game, the pupils are also introduced to the concept of a function of a function and the idea of an inverse function which can reverse the action of another function. Finally, we explore the concept of an irrational number which is always fun for mathematically gifted students who enjoy thinking about the idea of infinity.

This week opens with them exploring the idea that all fractions in their fully simplified form must contain an odd number in either their numerator or denominator. Therefore a fraction with two even numbers, like a zombie, does not really exist but is simply dressed up. We then teach the students how maths has certain syntaxial rules and from these rules algebraic behaviours are derived. We focus on how multiplying the same base variable (say x) together n times is recorded with the base raised by the number n (xn). We compare this to the rule of adding x together n times where n is written directly in front of the variable (nx). Using indices, we then show how division translates to a negative power and thus any number raised to the power 0 must be equal to 1. We then consider brackets and BODMAS and how one can show that n(x+y) can be expanded to remove the brackets such that n(x+y)=nx+ny. Finally, we end by introducing the students to two functions E=2n (the even integer function) and O=2n+1 (the odd integer function). If n is an integer, then these two functions generate even and odd integers respectively.

This is a rest week where we start with a Murder Mystery drama which will be used in week 5 to introduce the pupils to the concept of a proof by contradiction. In this drama, the hapless Watson assumes an old man has died of natural causes only to discover the evidence contradicts his assumption. He is guided by the great detective Holmes to correctly conclude that a young woman has been murdered (because of a dagger sticking out of her head) oops! We then continue with the Maths Rod trick where students learn how to instantly calculate 4 digit numbers that are formed when 4 rods are place together. Finally, we end with a bit of a maths themed Zumba where the exercises are determined by a mathematical calculation and the students keep track of their workout by recording what numbers came up on screen and so what exercises they were required to do and how many times they had to do them (see example worksheet on the right or above if viewing on a mobile phone).

We resume our quest to prove that √2 is an irrational number. We continue to hone our algebraic skills before proving that the square of all even integers are even integers while the square of all odd integers are odd integers by squaring the even integer (E=2n) and the odd integer function (O=2n+1) respectively. This means that if the square root of an even integer results in an integer, then that integer must be even. Likewise, if square root of an odd integer results in an integer, then that integer must also be odd.

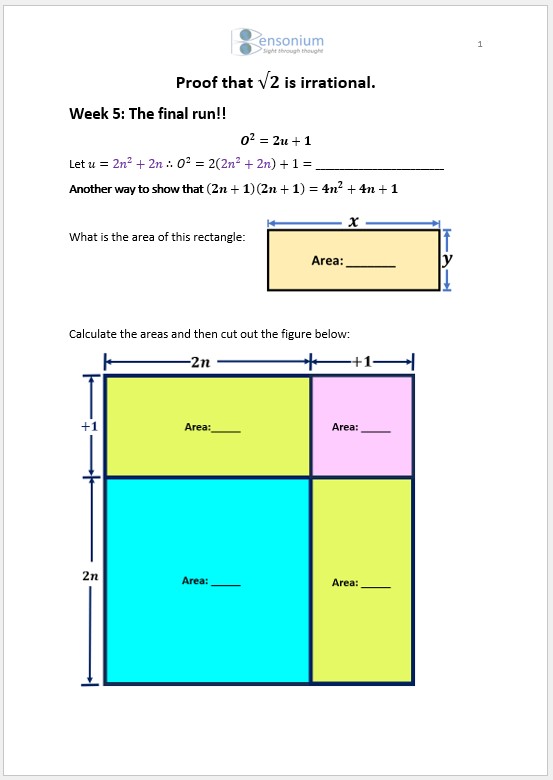Last week we proved that the square of an odd integer is an odd integer by expanding the odd integer function O=2n+1 (O2=4n2+4n+1). This week we work through another relatively easy to understand geometrical method of expanding this function. By cutting out and arranging shapes, where the area of each shape forms the answer to the expansion of (2n+1)2 the students learn another way to show this evaluates to 4n2+4n+1 which is always an odd integer if n is an integer. We now bring all our mathematical ingredients together to prove that √2 is an irrational number. First we assume that √2 can be written as a fraction and we let the numerator equal the unknown integer a and the denominator equal the unknown integer b such that √2=a/b. We now use the fact that if the square of all even integers are even integers and the square of all odd integers are odd integers then the square root of all even integers (which result in an integer) are also even integers. Using this fact we can prove that if √2 could be written in the form a/b then both a and b must be even integers. However, since fully factored fractions with two even integers don’t exist, our assumption has led us to a mathematical contradiction. Like Detective Watson in week 3, who after assuming an old man had died of natural causes discovered it was in fact a young woman who had been murdered, so we, after assuming we could write √2 down as a fraction discovered we couldn’t. Therefore √2 must be an irrational number.

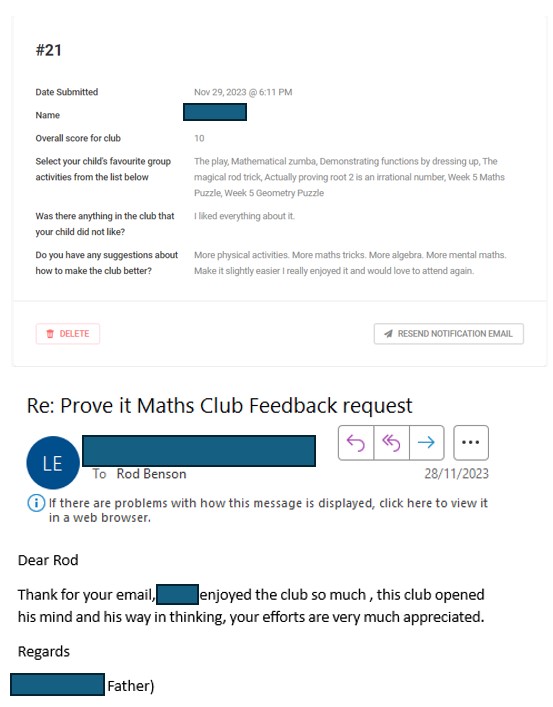At the end of the course the students each receive a certificate they can place on their bedroom walls. On the reverse side of the certificate is the complete proof that √2 is irrational. At the end of 2023, I ran a pilot of this club in a local Manchester Primary School for selected 5^th and 6^th grade students. This was only a small pilot club but all the feedback I got from it was positive and two examples (one from a student and one from a parent) are shown in the right panel or above if viewing on a mobile phone.